Load – load is a term frequently used in engineering to mean, the force exerted on a surface.
Stress – internal resistance force induced in component due to deformation under the action of loading, due to this load internal resistance force (I.R.F) created and body tends to regain its original shape if deformation tends up to elastic limit. This internal resistance force at a point called as stress, stress = internal resting force/unit area. Its unit is kg/mm2 or MPa -Stress = P/A (P-load acting on the component and A- cross sectional area of the components, Stress is denoted by letter σ (sigma).
Strain - when forces or loads act on a component, it undergoes some deformation. This deformation per unit length is known as strain it is a unitless quantity.
Strain is normally represented by letter e or ε (epsilon), change in length (dimension) is represented by Δl or δl (delta), strain = δl/l, l=length (original dimension)
Strain is developed in response to the stress produced. More the stress, more the strain.
Stress, Strain Curve –
In engineering and material science, a stress-strain curve for a material gives the relationship between stress and strain. It is obtained by gradually applying load to a test coupon and measuring the deformation, from which the stress and strain can be determined. These curves reveal many of the properties of a materials, such as the young’s modules, the yield strength and ultimate tensile strength.
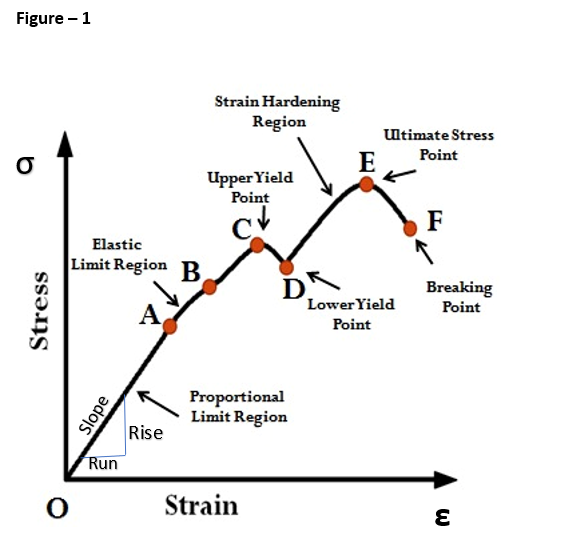
A schematic diagram for the stress-strain curve of low carbon steel is shown in figure -1. There are several stages showing different behaviors, which suggests different mechanical properties.
- Linear elastic region/proportional limit-
The first stage is the linear elastic region or proportional limit. The stress is proportional to strain (i.e. from O to A the straight line), that is, obeys the general hook’s law and the slope is young’s modulus. Beyond point A, the curve slightly deviates from the straight line. It is thus obvious that hook’s law holds good up to point A and it is known as proportional limit. It is defined as at that stress at which the stress-strain curve begins to deviate from the straight line.
- Elastic limit – note that even if the load is increased beyond point A up to point B, the material will regain its shape and size when load is removed. Means that the material has elastic properties up to the point B. this point is known as elastic limit. It is defined as the stress developed in the material without any permanent deformation. As the above two limits A and B are very close to each other, therefore, for all practical purposes these are taken to be equal.
- Yield point – if the material is stressed beyond point B, the plastic stage will reach, means on the removal of the load, the material will not regain its original shape or size. A little consideration will show that beyond point B, the strain increases at a faster rate with any increase in stress until the point C is reached. At this point, the material yields before the load and there is an appreciable strain without any increase in stress. In case of mild steel, it will be seen that a small load drops to D, immediately after yielding commences. Hence there are two yield points C and D. the points C and D are called the upper and lower yield points respectively. Corresponding stress to yield point is known as yield point stress (YS).
- Ultimate stress – At point D, the material regains some strength and higher values of stresses are required for higher strains, than those between A and D. the load goes on increasing till the point E is reached. The gradual increase in the strain (or length) of the specimen is followed with the uniform reduction of its cross-sectional area. The work done during the stretching the specimen is transferred largely into heat and the specimen becomes hot. At point E, the stress, which attains its maximum value is known as ultimate tensile stress (UTS). It is defined as the largest stress obtained by dividing the largest value of the load reached in a test to the original cross-sectional area of the test piece.
- Breaking stress – once the specimen has reached the ultimate stress, a neck is formed, which decreases the cross-sectional area of the specimen, as shown in figure-2B. A little consideration will show that the stress (or load) necessary to break the specimen, is less than the maximum stress. The stress is therefore, reduced until the specimen breaks at point F. the stress corresponding to point F is known as breaking stress.
